| English | 简体中文 |
1719. Number Of Ways To Reconstruct A Tree
Description
You are given an array pairs, where pairs[i] = [xi, yi], and:
- There are no duplicates.
xi < yi
Let ways be the number of rooted trees that satisfy the following conditions:
- The tree consists of nodes whose values appeared in
pairs. - A pair
[xi, yi]exists inpairsif and only ifxiis an ancestor ofyioryiis an ancestor ofxi. - Note: the tree does not have to be a binary tree.
Two ways are considered to be different if there is at least one node that has different parents in both ways.
Return:
0ifways == 01ifways == 12ifways > 1
A rooted tree is a tree that has a single root node, and all edges are oriented to be outgoing from the root.
An ancestor of a node is any node on the path from the root to that node (excluding the node itself). The root has no ancestors.
Example 1:
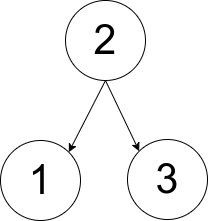
Input: pairs = [[1,2],[2,3]] Output: 1 Explanation: There is exactly one valid rooted tree, which is shown in the above figure.
Example 2:

Input: pairs = [[1,2],[2,3],[1,3]] Output: 2 Explanation: There are multiple valid rooted trees. Three of them are shown in the above figures.
Example 3:
Input: pairs = [[1,2],[2,3],[2,4],[1,5]] Output: 0 Explanation: There are no valid rooted trees.
Constraints:
1 <= pairs.length <= 1051 <= xi < yi <= 500- The elements in
pairsare unique.